Who Created The Planetary Model

Atomic model introduced by Niels Bohr in 1913

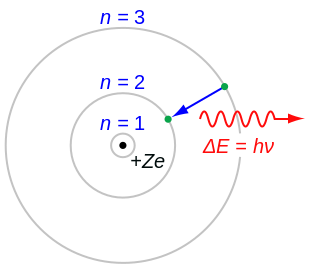
The block model of the hydrogen cantlet ( Z = 1) or a hydrogen-similar ion ( Z > 1), where the negatively charged electron confined to an diminutive shell encircles a small, positively charged atomic nucleus and where an electron jumps between orbits, is accompanied by an emitted or captivated corporeality of electromagnetic energy (hν).^[ane] The orbits in which the electron may travel are shown as grayness circles; their radius increases as north ^two, where n is the chief breakthrough number. The 3 → ii transition depicted here produces the beginning line of the Balmer series, and for hydrogen ( Z = ane) it results in a photon of wavelength 656 nm (red light).

In atomic physics, the Bohr model or Rutherford–Bohr model, presented by Niels Bohr and Ernest Rutherford in 1913, is a system consisting of a small, dense nucleus surrounded by orbiting electrons—similar to the construction of the Solar Organization, but with attraction provided by electrostatic forces in place of gravity. It came afterwards the solar arrangement Joseph Larmor model (1897), the cubical model (1902), the Hantaro Nagaoka Saturnian model (1904), the plum pudding model (1904), the quantum Arthur Haas model (1910), the Rutherford model (1911), and the nuclear breakthrough John William Nicholson model (1912). The comeback over the 1911 Rutherford model mainly concerned the new quantum physical estimation introduced past Haas and Nicholson, just forsaking whatever attempt to align with classical physics radiation.

The model'southward key success lay in explaining the Rydberg formula for the spectral emission lines of atomic hydrogen. While the Rydberg formula had been known experimentally, it did non gain a theoretical underpinning until the Bohr model was introduced. Not only did the Bohr model explain the reasons for the structure of the Rydberg formula, it also provided a justification for the cardinal physical constants that make up the formula's empirical results.

The Bohr model is a relatively primitive model of the hydrogen atom, compared to the valence crush cantlet model. As a theory, it can be derived as a first-society approximation of the hydrogen atom using the broader and much more authentic quantum mechanics and thus may exist considered to be an obsolete scientific theory. Notwithstanding, considering of its simplicity, and its correct results for selected systems (run across beneath for application), the Bohr model is still ordinarily taught to introduce students to quantum mechanics or energy level diagrams before moving on to the more accurate, but more circuitous, valence beat cantlet. A related quantum model was originally proposed past Arthur Erich Haas in 1910 only was rejected until the 1911 Solvay Congress where it was thoroughly discussed.^[2] The quantum theory of the menstruation between Planck's discovery of the quantum (1900) and the advent of a mature quantum mechanics (1925) is frequently referred to as the sometime quantum theory.

Origin [edit]

Bohr model in 1921^[iii] later Sommerfeld expansion of 1913 model showing maximum electrons per crush with shells labeled in X-ray notation

In the early 20th century, experiments by Ernest Rutherford established that atoms consisted of a diffuse cloud of negatively charged electrons surrounding a small-scale, dense, positively charged nucleus.^[four] Given this experimental data, Rutherford naturally considered a planetary model of the cantlet, the Rutherford model of 1911. This had electrons orbiting a solar nucleus, but involved a technical difficulty: the laws of classical mechanics (i.e. the Larmor formula) predict that the electron volition release electromagnetic radiation while orbiting a nucleus. Because the electron would lose energy, it would rapidly spiral inwards, collapsing into the nucleus on a timescale of around 16 picoseconds.^[5] Rutherford'south atom model is disastrous considering it predicts that all atoms are unstable.^[half-dozen] Too, equally the electron spirals inward, the emission would rapidly increase in frequency due to the orbital menses condign shorter, resulting in electromagnetic radiation with a continuous spectrum. However, late 19th-century experiments with electric discharges had shown that atoms will only emit lite (that is, electromagnetic radiation) at certain detached frequencies. Past the early twentieth century, information technology was expected that the atom would account for the spectral lines. In 1897, Lord Rayleigh analyzed the problem. By 1906, Rayleigh said, "the frequencies observed in the spectrum may not be frequencies of disturbance or of oscillation in the ordinary sense at all, but rather form an essential function of the original constitution of the atom as determined by conditions of stability."^{[7] [8]}

The outline of Bohr's atom came during the proceedings of the first Solvay Conference in 1911 on the subject of Radiation and Quanta, at which Bohr'south mentor, Rutherford was present. Max Planck's lecture ended with this remark: "... atoms or electrons subject to the molecular bond would obey the laws of quantum theory".^{[9] [10]} Hendrik Lorentz in the discussion of Planck's lecture raised the question of the limerick of the cantlet based on Thomson's model with a swell portion of the discussion around the diminutive model developed by Arthur Erich Haas. Lorentz explained that Planck's constant could be taken equally determining the size of atoms, or that the size of atoms could be taken to determine Planck'due south constant.^[11] Lorentz included comments regarding the emission and absorption of radiation concluding that "A stationary state will be established in which the number of electrons entering their spheres is equal to the number of those leaving them."^[two] In the discussion of what could regulate energy differences between atoms, Max Planck just stated: "The intermediaries could be the electrons."^[12] The discussions outlined the need for the breakthrough theory to be included in the atom and the difficulties in an atomic theory. Planck in his talk said explicitly: "In order for an oscillator [molecule or cantlet] to exist able to provide radiation in accordance with the equation, it is necessary to introduce into the laws of its performance, as we have already said at the starting time of this Study, a particular physical hypothesis which is, on a primal betoken, in contradiction with classical Mechanics, explicitly or tacitly."^[13] Bohr's first paper on his atomic model quotes Planck nigh word for word, saying: "Whatever the alteration in the laws of motion of the electrons may be, it seems necessary to innovate in the laws in question a quantity strange to the classical electrodynamics, i. e. Planck's constant, or as information technology often is chosen the elementary quantum of activeness." Bohr's footnote at the bottom of the page is to the French translation of the 1911 Solvay Congress proving he patterned his model directly on the proceedings and fundamental principles laid down past Planck, Lorentz, and the quantized Arthur Haas model of the atom which was mentioned seventeen times.^[four] Lorentz ended the discussion of Einstein's talk explaining: "The assumption that this energy must exist a multiple of ${\displaystyle h\nu }$ leads to the post-obit formula, where ${\displaystyle due north}$ is an integer: ${\displaystyle qv^{2}=nh\nu }$ ."^[14] Rutherford could accept outlined these points to Bohr or given him a copy of the proceedings since he quoted from them and used them every bit a reference.^[15] In a later interview, Bohr said information technology was very interesting to hear Rutherford's remarks almost the Solvay Congress.^[16] But Bohr said, "I saw the actual reports" of the Solvay Congress.^[17]

Then in 1912, Bohr came across the John William Nicholson theory of the atom model that quantized angular momentum every bit h/2π. According to a centennial celebration of the Bohr atom in Nature magazine, information technology was Nicholson who discovered that electrons radiate the spectral lines equally they descend towards the nucleus and his theory was both nuclear and quantum.^{[10] [eighteen] [19]} Niels Bohr quoted him in his 1913 paper of the Bohr model of the atom.^[iv] The importance of the work of Nicholson's nuclear quantum atomic model on Bohr'south model has been emphasized past many historians.^{[20] [21] [19] [22]}

Next, Bohr was told by his friend, Hans Hansen, that the Balmer serial is calculated using the Balmer formula, an empirical equation discovered by Johann Balmer in 1885 that described wavelengths of some spectral lines of hydrogen.^{[16] [23]} This was further generalized by Johannes Rydberg in 1888 resulting in what is at present known as the Rydberg formula. Later on this, Bohr declared, "everything became clear".^[23]

To overcome the problems of Rutherford's atom, in 1913 Niels Bohr put forth iii postulates that sum up most of his model:

1. The electron is able to revolve in certain stable orbits effectually the nucleus without radiating any free energy, contrary to what classical electromagnetism suggests. These stable orbits are called stationary orbits and are attained at sure discrete distances from the nucleus. The electron cannot take whatsoever other orbit in between the discrete ones.
2. The stationary orbits are attained at distances for which the angular momentum of the revolving electron is an integer multiple of the reduced Planck abiding: ${\displaystyle m_{\mathrm {eastward} }vr=n\hbar }$ , where n = 1, 2, 3, ... is chosen the principal breakthrough number, and ħ = h/2π . The lowest value of northward is one; this gives the smallest possible orbital radius of 0.0529 nm known every bit the Bohr radius. Once an electron is in this lowest orbit, it tin can go no closer to the nucleus. Starting from the athwart momentum breakthrough rule every bit Bohr admits is previously given by Nicholson in his 1912 paper,^{[16] [x] [18] [nineteen]} Bohr^[iv] was able to calculate the energies of the allowed orbits of the hydrogen atom and other hydrogen-similar atoms and ions. These orbits are associated with definite energies and are also called energy shells or energy levels. In these orbits, the electron's acceleration does not result in radiation and energy loss. The Bohr model of an atom was based upon Planck'south breakthrough theory of radiation.
3. Electrons can merely gain and lose energy by jumping from one immune orbit to some other, arresting or emitting electromagnetic radiation with a frequency ν adamant past the energy difference of the levels co-ordinate to the Planck relation: ${\displaystyle \Delta East=E_{two}-E_{i}=h\nu }$ , where h is Planck'due south constant.

Other points are:

1. Like Einstein'southward theory of the photoelectric consequence, Bohr's formula assumes that during a quantum jump a discrete corporeality of free energy is radiated. All the same, dissimilar Einstein, Bohr stuck to the classical Maxwell theory of the electromagnetic field. Quantization of the electromagnetic field was explained by the discreteness of the atomic energy levels; Bohr did non believe in the existence of photons.^{[24] [25]}
2. Co-ordinate to the Maxwell theory the frequency ν of classical radiations is equal to the rotation frequency ν _rot of the electron in its orbit, with harmonics at integer multiples of this frequency. This result is obtained from the Bohr model for jumps between energy levels E _n and East _n−k when chiliad is much smaller than n. These jumps reproduce the frequency of the one thousand-th harmonic of orbit n. For sufficiently large values of n (and so-called Rydberg states), the two orbits involved in the emission process have nearly the same rotation frequency, so that the classical orbital frequency is not cryptic. But for small n (or large grand), the radiation frequency has no unambiguous classical interpretation. This marks the birth of the correspondence principle, requiring quantum theory to hold with the classical theory simply in the limit of large quantum numbers.
3. The Bohr–Kramers–Slater theory (BKS theory) is a failed attempt to extend the Bohr model, which violates the conservation of energy and momentum in quantum jumps, with the conservation laws only property on average.

Bohr's condition, that the angular momentum is an integer multiple of ħ was later on reinterpreted in 1924 by de Broglie as a standing wave condition: the electron is described by a wave and a whole number of wavelengths must fit along the circumference of the electron'south orbit:

${\displaystyle n\lambda =2\pi r.}$

Co-ordinate to de Broglie's hypothesis, matter particles such every bit the electron behave equally waves. The de Broglie wavelength of an electron is

${\displaystyle \lambda ={\frac {h}{mv}},}$

which implies that

${\displaystyle {\frac {nh}{mv}}=2\pi r,}$

or

${\displaystyle {\frac {nh}{ii\pi }}=mvr,}$

where ${\displaystyle mvr}$ is the angular momentum of the orbiting electron. Writing ${\displaystyle \ell }$ for this angular momentum, the previous equation becomes

${\displaystyle \ell ={\frac {nh}{2\pi }},}$

which is Bohr'due south second postulate.

Bohr described angular momentum of the electron orbit every bit 1/2h while de Broglie's wavelength of λ = h/p described h divided by the electron momentum. In 1913, withal, Bohr justified his rule by appealing to the correspondence principle, without providing any sort of wave interpretation. In 1913, the wave behavior of thing particles such as the electron was non suspected.

In 1925, a new kind of mechanics was proposed, breakthrough mechanics, in which Bohr'south model of electrons traveling in quantized orbits was extended into a more accurate model of electron movement. The new theory was proposed by Werner Heisenberg. Some other class of the same theory, wave mechanics, was discovered by the Austrian physicist Erwin Schrödinger independently, and by unlike reasoning. Schrödinger employed de Broglie's matter waves, just sought wave solutions of a three-dimensional wave equation describing electrons that were constrained to motion about the nucleus of a hydrogen-similar cantlet, by being trapped by the potential of the positive nuclear charge.

Electron energy levels [edit]

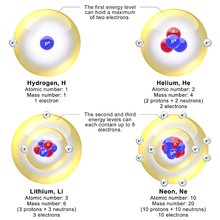
Models depicting electron energy levels in hydrogen, helium, lithium, and neon

The Bohr model gives nearly exact results but for a system where two charged points orbit each other at speeds much less than that of light. This not just involves i-electron systems such every bit the hydrogen atom, singly ionized helium, and doubly ionized lithium, simply information technology includes positronium and Rydberg states of any cantlet where one electron is far abroad from everything else. It tin can exist used for K-line X-ray transition calculations if other assumptions are added (come across Moseley's police force below). In high energy physics, it can be used to calculate the masses of heavy quark mesons.

Calculation of the orbits requires ii assumptions.

• Classical mechanics

The electron is held in a round orbit by electrostatic attraction. The centripetal forcefulness is equal to the Coulomb force.

${\displaystyle {\frac {m_{\mathrm {e} }v^{2}}{r}}={\frac {Zk_{\mathrm {due east} }due east^{2}}{r^{2}}},}$

where thou _{due east} is the electron'due south mass, e is the elementary accuse, k _e is the Coulomb abiding and Z is the atom's atomic number. It is causeless here that the mass of the nucleus is much larger than the electron mass (which is a skillful assumption). This equation determines the electron'southward speed at any radius:

${\displaystyle v={\sqrt {\frac {Zk_{\mathrm {e} }eastward^{ii}}{m_{\mathrm {e} }r}}}.}$

Information technology also determines the electron's full energy at whatsoever radius:

${\displaystyle E=-{\frac {1}{two}}m_{\mathrm {eastward} }v^{ii}.}$

The total energy is negative and inversely proportional to r. This ways that it takes energy to pull the orbiting electron away from the proton. For space values of r, the energy is zero, corresponding to a motionless electron infinitely far from the proton. The total energy is half the potential energy, the departure being the kinetic free energy of the electron. This is too true for noncircular orbits by the virial theorem.

• A breakthrough rule

The athwart momentum L = m _e vr is an integer multiple of ħ:

${\displaystyle m_{\mathrm {e} }vr=north\hbar .}$

Derivation [edit]

If an electron in an atom is moving on an orbit with period T, classically the electromagnetic radiation will repeat itself every orbital menstruum. If the coupling to the electromagnetic field is weak, then that the orbit doesn't decay very much in one cycle, the radiation will be emitted in a pattern which repeats every period, so that the Fourier transform will have frequencies which are only multiples of 1/T. This is the classical radiation law: the frequencies emitted are integer multiples of 1/T.

In quantum mechanics, this emission must exist in quanta of light, of frequencies consisting of integer multiples of ane/T, so that classical mechanics is an approximate description at large quantum numbers. This means that the energy level corresponding to a classical orbit of period 1/T must have nearby energy levels which differ in energy by h/T, and they should be equally spaced near that level,

${\displaystyle \Delta E_{n}={\frac {h}{T(E_{n})}}.}$

Bohr worried whether the energy spacing 1/T should be best calculated with the menses of the energy state ${\displaystyle E_{n}}$ , or ${\displaystyle E_{n+1}}$ , or some average—in hindsight, this model is only the leading semiclassical approximation.

Bohr considered circular orbits. Classically, these orbits must disuse to smaller circles when photons are emitted. The level spacing between round orbits tin be calculated with the correspondence formula. For a Hydrogen cantlet, the classical orbits have a period T determined past Kepler's 3rd constabulary to calibration as r ^3/2. The energy scales as 1/r, so the level spacing formula amounts to

${\displaystyle \Delta East\propto {\frac {i}{r^{three/ii}}}\propto East^{three/2}.}$

It is possible to determine the energy levels past recursively stepping down orbit by orbit, merely at that place is a shortcut.

The angular momentum Fifty of the circular orbit scales as ${\displaystyle {\sqrt {r}}}$ . The energy in terms of the angular momentum is so

${\displaystyle Due east\propto {\frac {1}{r}}\propto {\frac {1}{L^{2}}}.}$

Assuming, with Bohr, that quantized values of Fifty are equally spaced, the spacing between neighboring energies is

${\displaystyle \Delta E\propto {\frac {i}{(Fifty+\hbar )^{ii}}}-{\frac {1}{L^{2}}}\approx -{\frac {2\hbar }{L^{3}}}\propto -E^{iii/ii}.}$

This is equally desired for equally spaced angular momenta. If one kept track of the constants, the spacing would be ħ, so the athwart momentum should exist an integer multiple of ħ,

${\displaystyle L={\frac {nh}{ii\pi }}=n\hbar .}$

This is how Bohr arrived at his model.

Substituting the expression for the velocity gives an equation for r in terms of n:

${\displaystyle m_{\text{e}}{\sqrt {\dfrac {k_{\text{e}}Ze^{ii}}{m_{\text{e}}r}}}r=due north\hbar ,}$

so that the allowed orbit radius at any n is

${\displaystyle r_{northward}={\frac {n^{2}\hbar ^{two}}{Zk_{\mathrm {e} }eastward^{two}m_{\mathrm {east} }}}.}$

The smallest possible value of r in the hydrogen atom ( Z = i) is chosen the Bohr radius and is equal to:

${\displaystyle r_{1}={\frac {\hbar ^{2}}{k_{\mathrm {east} }e^{two}m_{\mathrm {e} }}}\approx 5.29\times x^{-eleven}~\mathrm {m} .}$

The energy of the n-th level for whatever cantlet is determined past the radius and quantum number:

${\displaystyle E=-{\frac {Zk_{\mathrm {due east} }e^{ii}}{2r_{north}}}=-{\frac {Z^{2}(k_{\mathrm {east} }e^{2})^{2}m_{\mathrm {east} }}{2\hbar ^{2}northward^{2}}}\approx {\frac {-13.6Z^{2}}{n^{ii}}}~\mathrm {eV} .}$

An electron in the everyman energy level of hydrogen ( n = 1) therefore has nearly 13.6 eV less energy than a motionless electron infinitely far from the nucleus. The side by side energy level ( due north = 2) is −iii.4 eV. The third ( n = three) is −1.51 eV, and then on. For larger values of north, these are as well the binding energies of a highly excited atom with 1 electron in a large circular orbit around the residual of the atom. The hydrogen formula also coincides with the Wallis product.^[26]

The combination of natural constants in the energy formula is called the Rydberg energy (R _Eastward):

${\displaystyle R_{\mathrm {East} }={\frac {(k_{\mathrm {e} }east^{2})^{2}m_{\mathrm {due east} }}{2\hbar ^{2}}}.}$

This expression is antiseptic past interpreting it in combinations that form more natural units:

${\displaystyle m_{\mathrm {e} }c^{2}}$ is the residual mass energy of the electron (511 keV),

${\displaystyle {\frac {k_{\mathrm {east} }east^{2}}{\hbar c}}=\alpha \approx {\frac {1}{137}}}$ is the fine-structure abiding,

${\displaystyle R_{\mathrm {E} }={\frac {i}{2}}(m_{\mathrm {e} }c^{2})\alpha ^{ii}}$ .

Since this derivation is with the supposition that the nucleus is orbited by one electron, we tin can generalize this result by letting the nucleus have a charge q = Ze , where Z is the diminutive number. This will now give us energy levels for hydrogenic (hydrogen-like) atoms, which tin serve as a rough order-of-magnitude approximation of the actual energy levels. So for nuclei with Z protons, the energy levels are (to a crude approximation):

${\displaystyle E_{north}=-{\frac {Z^{2}R_{\mathrm {Due east} }}{n^{2}}}.}$

The actual energy levels cannot exist solved analytically for more than one electron (see n-trunk trouble) because the electrons are non only affected past the nucleus but as well interact with each other via the Coulomb Forcefulness.

When Z = 1/α ( Z ≈ 137), the motion becomes highly relativistic, and Z ² cancels the α ^two in R; the orbit energy begins to be comparable to rest energy. Sufficiently big nuclei, if they were stable, would reduce their charge past creating a bound electron from the vacuum, ejecting the positron to infinity. This is the theoretical phenomenon of electromagnetic accuse screening which predicts a maximum nuclear charge. Emission of such positrons has been observed in the collisions of heavy ions to create temporary super-heavy nuclei.^[27]

The Bohr formula properly uses the reduced mass of electron and proton in all situations, instead of the mass of the electron,

${\displaystyle m_{\text{red}}={\frac {m_{\mathrm {e} }m_{\mathrm {p} }}{m_{\mathrm {e} }+m_{\mathrm {p} }}}=m_{\mathrm {e} }{\frac {1}{1+m_{\mathrm {east} }/m_{\mathrm {p} }}}.}$

Yet, these numbers are very nearly the aforementioned, due to the much larger mass of the proton, about 1836.1 times the mass of the electron, so that the reduced mass in the organization is the mass of the electron multiplied by the constant 1836.i/(1+1836.1) = 0.99946. This fact was historically important in disarming Rutherford of the importance of Bohr's model, for information technology explained the fact that the frequencies of lines in the spectra for singly ionized helium do not differ from those of hydrogen past a gene of exactly 4, but rather by iv times the ratio of the reduced mass for the hydrogen vs. the helium systems, which was much closer to the experimental ratio than exactly 4.

For positronium, the formula uses the reduced mass also, but in this case, it is exactly the electron mass divided past 2. For any value of the radius, the electron and the positron are each moving at half the speed around their common center of mass, and each has only ane 4th the kinetic free energy. The total kinetic energy is half what it would be for a single electron moving effectually a heavy nucleus.

${\displaystyle E_{n}={\frac {R_{\mathrm {E} }}{2n^{2}}}}$  (positronium).

Rydberg formula [edit]

The Rydberg formula, which was known empirically earlier Bohr'due south formula, is seen in Bohr'south theory as describing the energies of transitions or quantum jumps between orbital energy levels. Bohr's formula gives the numerical value of the already-known and measured the Rydberg abiding, but in terms of more than cardinal constants of nature, including the electron's charge and the Planck constant.

When the electron gets moved from its original energy level to a college ane, it then jumps back each level until information technology comes to the original position, which results in a photon being emitted. Using the derived formula for the different energy levels of hydrogen 1 may determine the wavelengths of low-cal that a hydrogen atom can emit.

The energy of a photon emitted by a hydrogen atom is given by the difference of two hydrogen energy levels:

${\displaystyle E=E_{i}-E_{f}=R_{\text{Due east}}\left({\frac {1}{n_{f}^{two}}}-{\frac {1}{n_{i}^{ii}}}\correct),}$

where n _f is the concluding free energy level, and n _i is the initial free energy level.

Since the energy of a photon is

${\displaystyle E={\frac {hc}{\lambda }},}$

the wavelength of the photon given off is given by

${\displaystyle {\frac {1}{\lambda }}=R\left({\frac {i}{n_{f}^{2}}}-{\frac {1}{n_{i}^{2}}}\right).}$

This is known as the Rydberg formula, and the Rydberg abiding R is R _{Due east}/hc , or R _E/2π in natural units. This formula was known in the nineteenth century to scientists studying spectroscopy, merely in that location was no theoretical caption for this form or a theoretical prediction for the value of R , until Bohr. In fact, Bohr's derivation of the Rydberg constant, besides as the concomitant agreement of Bohr's formula with experimentally observed spectral lines of the Lyman ( n_f =i), Balmer ( n_f =2), and Paschen ( due north_f =three) series, and successful theoretical prediction of other lines non yet observed, was one reason that his model was immediately accepted.

To utilise to atoms with more than 1 electron, the Rydberg formula tin can be modified past replacing Z with Z −b or n with northward −b where b is abiding representing a screening effect due to the inner-shell and other electrons (run across Electron shell and the later discussion of the "Shell Model of the Atom" below). This was established empirically before Bohr presented his model.

Shell model (heavier atoms) [edit]

Bohr's original three papers in 1913 described mainly the electron configuration in lighter elements. Bohr chosen his electron shells, "rings" in 1913. Diminutive orbitals within shells did not exist at the time of his planetary model. Bohr explains in Part 3 of his famous 1913 paper that the maximum electrons in a beat out is eight, writing: "We see, further, that a band of n electrons cannot rotate in a unmarried ring round a nucleus of charge n_eastward unless n < 8." For smaller atoms, the electron shells would be filled as follows: "rings of electrons volition only join together if they contain equal numbers of electrons; and that accordingly the numbers of electrons on inner rings will just exist two, four, 8". However, in larger atoms the innermost beat would incorporate eight electrons, "on the other hand, the periodic system of the elements strongly suggests that already in neon N = 10 an inner ring of eight electrons will occur". Meet periodic table for more nigh how Bohr built his 1913 model of electrons in elements

"From the higher up we are led to the post-obit possible scheme for the system of the electrons in light atoms:

Chemical element	Electrons per shell
iv	2, 2
half-dozen	2, 4
vii	4, 3
8	4, 2, 2
9	four, four, 1
ten	8, 2
xi	8, 2, 1
sixteen	8, 4, 2, 2
xviii	eight, viii, 2

Periodic table of Bohr in 1913 showing electron configurations in his 2nd newspaper where he went to the 24th element.^{[28] [3] [15]} In Bohr's third 1913 newspaper Part Three called systems containing several nuclei, he says that two atoms form molecules on a symmetrical plane and he reverts to describing Hydrogen.^[29] The 1913 Bohr model did not talk over higher elements in particular and John William Nicholson was one of the first to prove in 1914 that it couldn't work for Lithium, only was an attractive theory for Hydrogen and ionized helium.^{[15] [30]}

In 1921, following the work of chemists and others involved in piece of work on the periodic tabular array, Bohr extended the model of hydrogen to give an approximate model for heavier atoms. This gave a physical picture that reproduced many known atomic properties for the start fourth dimension although these properties were proposed contemporarily with the identical work of pharmacist Charles Rugeley Coffin^{[3] [31]}

Bohr'due south partner in research during 1914 to 1916 was Walther Kossel who corrected Bohr's work to testify that electrons interacted through the outer rings, and Kossel called the rings: "shells."^{[32] [33]} Irving Langmuir is credited with the first feasible system of electrons in shells with only two in the beginning shell and going upwardly to eight in the next according to the octet rule of 1904, although Kossel had already predicted a maximum of eight per shell in 1916.^[34] Heavier atoms have more protons in the nucleus, and more electrons to abolish the accuse. Bohr took from these chemists the idea that each discrete orbit could only concur a sure number of electrons. Per Kossel, afterward that the orbit is full, the next level would have to exist used.^[three] This gives the atom a crush construction designed past Kossel, Langmuir, and Bury, in which each shell corresponds to a Bohr orbit.

This model is even more approximate than the model of hydrogen, because information technology treats the electrons in each shell every bit not-interacting. But the repulsions of electrons are taken into business relationship somewhat by the phenomenon of screening. The electrons in outer orbits exercise non only orbit the nucleus, just they also move effectually the inner electrons, then the effective charge Z that they feel is reduced by the number of the electrons in the inner orbit.

For example, the lithium atom has two electrons in the lowest 1s orbit, and these orbit at Z = 2. Each one sees the nuclear charge of Z = 3 minus the screening result of the other, which crudely reduces the nuclear charge by i unit. This means that the innermost electrons orbit at approximately one/2 the Bohr radius. The outermost electron in lithium orbits at roughly the Bohr radius, since the ii inner electrons reduce the nuclear charge by 2. This outer electron should be at almost one Bohr radius from the nucleus. Considering the electrons strongly repel each other, the effective charge description is very approximate; the effective charge Z doesn't usually come up out to exist an integer. Merely Moseley'southward constabulary experimentally probes the innermost pair of electrons, and shows that they do see a nuclear charge of approximately Z − 1, while the outermost electron in an atom or ion with merely 1 electron in the outermost shell orbits a core with constructive charge Z −m where chiliad is the full number of electrons in the inner shells.

The shell model was able to qualitatively explain many of the mysterious properties of atoms which became codification in the late 19th century in the periodic table of the elements. One property was the size of atoms, which could be determined approximately by measuring the viscosity of gases and density of pure crystalline solids. Atoms tend to get smaller toward the right in the periodic table, and go much larger at the next line of the table. Atoms to the right of the table tend to gain electrons, while atoms to the left tend to lose them. Every element on the last cavalcade of the table is chemically inert (noble gas).

In the shell model, this phenomenon is explained past beat out-filling. Successive atoms go smaller because they are filling orbits of the aforementioned size, until the orbit is full, at which point the next atom in the table has a loosely jump outer electron, causing it to aggrandize. The outset Bohr orbit is filled when it has ii electrons, which explains why helium is inert. The second orbit allows eight electrons, and when information technology is total the atom is neon, again inert. The third orbital contains 8 again, except that in the more right Sommerfeld treatment (reproduced in modernistic quantum mechanics) in that location are extra "d" electrons. The third orbit may hold an actress 10 d electrons, but these positions are non filled until a few more orbitals from the next level are filled (filling the due north=iii d orbitals produces the 10 transition elements). The irregular filling design is an effect of interactions between electrons, which are not taken into account in either the Bohr or Sommerfeld models and which are difficult to calculate even in the modern treatment.

Moseley'south law and calculation (G-blastoff X-ray emission lines) [edit]

Niels Bohr said in 1962: "You see actually the Rutherford work was not taken seriously. We cannot understand today, but it was not taken seriously at all. There was no mention of information technology whatsoever place. The great change came from Moseley."^[35]

In 1913, Henry Moseley found an empirical human relationship between the strongest X-ray line emitted past atoms under electron bombardment (then known as the Grand-alpha line), and their atomic number Z . Moseley's empiric formula was found to exist derivable from Rydberg's formula and later Bohr's formula (Moseley actually mentions just Ernest Rutherford and Antonius Van den Broek in terms of models equally these had been published before Moseley's work and Moseley'due south 1913 paper was published the aforementioned calendar month as the first Bohr model paper).^[36] The two boosted assumptions that [1] this X-ray line came from a transition between energy levels with quantum numbers 1 and 2, and [two], that the atomic number Z when used in the formula for atoms heavier than hydrogen, should be diminished past 1, to (Z − one)² .

Moseley wrote to Bohr, puzzled about his results, but Bohr was non able to help. At that time, he thought that the postulated innermost "Chiliad" shell of electrons should take at least 4 electrons, not the two which would have neatly explained the result. So Moseley published his results without a theoretical explanation.

It was Walther Kossel in 1914 and in 1916 who explained that in the periodic table new elements would be created equally electrons were added to the outer beat. In Kossel'south paper, he writes: "This leads to the conclusion that the electrons, which are added further, should be put into concentric rings or shells, on each of which ... but a certain number of electrons—namely, eight in our case—should exist arranged. As soon as one ring or shell is completed, a new one has to exist started for the next chemical element; the number of electrons, which are most easily accessible, and lie at the outermost periphery, increases again from element to element and, therefore, in the formation of each new shell the chemical periodicity is repeated."^{[32] [33]} Later, chemist Langmuir realized that the upshot was caused past charge screening, with an inner beat containing only 2 electrons. In his 1919 paper, Irving Langmuir postulated the beingness of "cells" which could each only contain 2 electrons each, and these were arranged in "equidistant layers".

In the Moseley experiment, 1 of the innermost electrons in the atom is knocked out, leaving a vacancy in the lowest Bohr orbit, which contains a single remaining electron. This vacancy is then filled past an electron from the side by side orbit, which has north=2. But the n=2 electrons meet an effective charge of Z − 1, which is the value appropriate for the charge of the nucleus, when a single electron remains in the lowest Bohr orbit to screen the nuclear accuse +Z, and lower it by −1 (due to the electron's negative charge screening the nuclear positive charge). The free energy gained by an electron dropping from the 2d shell to the first gives Moseley'south police force for K-blastoff lines,

${\displaystyle E=h\nu =E_{i}-E_{f}=R_{\mathrm {Due east} }(Z-ane)^{ii}\left({\frac {1}{1^{two}}}-{\frac {one}{two^{2}}}\right),}$

or

${\displaystyle f=\nu =R_{\mathrm {v} }\left({\frac {3}{iv}}\right)(Z-1)^{ii}=(2.46\times x^{15}~{\text{Hz}})(Z-1)^{2}.}$

Here, R _v = R _E/h is the Rydberg abiding, in terms of frequency equal to iii.28 ten x^xv Hz. For values of Z between 11 and 31 this latter relationship had been empirically derived by Moseley, in a simple (linear) plot of the square root of X-ray frequency against atomic number (however, for argent, Z = 47, the experimentally obtained screening term should be replaced past 0.iv). Notwithstanding its restricted validity,^[37] Moseley's law non just established the objective meaning of atomic number, but equally Bohr noted, it besides did more than the Rydberg derivation to found the validity of the Rutherford/Van den Broek/Bohr nuclear model of the cantlet, with diminutive number (identify on the periodic tabular array) standing for whole units of nuclear charge. Van den Broek had published his model in January 1913 showing the periodic table was arranged co-ordinate to charge while Bohr's atomic model was non published until July 1913.^[38]

The M-blastoff line of Moseley'south time is now known to be a pair of close lines, written equally (Kα₁ and Kα₂ ) in Siegbahn notation.

Shortcomings [edit]

The Bohr model gives an incorrect value Fifty=ħ for the ground state orbital angular momentum: The angular momentum in the true ground state is known to be zero from experiment.^[39] Although mental pictures fail somewhat at these levels of scale, an electron in the lowest mod "orbital" with no orbital momentum, may be thought of as not to rotate "around" the nucleus at all, but simply to go tightly around it in an ellipse with nothing expanse (this may be pictured as "back and along", without hit or interacting with the nucleus). This is but reproduced in a more sophisticated semiclassical treatment similar Sommerfeld'due south. Still, even the most sophisticated semiclassical model fails to explain the fact that the everyman energy land is spherically symmetric – it doesn't signal in whatsoever detail management.

Nevertheless, in the modern fully quantum treatment in phase space, the proper deformation (conscientious full extension) of the semi-classical result adjusts the athwart momentum value to the correct constructive one.^[40] As a consequence, the concrete ground state expression is obtained through a shift of the vanishing quantum athwart momentum expression, which corresponds to spherical symmetry.

In modernistic quantum mechanics, the electron in hydrogen is a spherical deject of probability that grows denser near the nucleus. The rate-abiding of probability-decay in hydrogen is equal to the inverse of the Bohr radius, but since Bohr worked with circular orbits, not nothing area ellipses, the fact that these ii numbers exactly agree is considered a "coincidence". (However, many such casual agreements are plant between the semiclassical vs. full breakthrough mechanical treatment of the atom; these include identical energy levels in the hydrogen atom and the derivation of a fine-structure constant, which arises from the relativistic Bohr–Sommerfeld model (come across below) and which happens to exist equal to an entirely unlike concept, in full modern breakthrough mechanics).

The Bohr model likewise has difficulty with, or else fails to explicate:

• Much of the spectra of larger atoms. At best, it can make predictions most the Yard-alpha and some L-alpha X-ray emission spectra for larger atoms, if two boosted advertisement hoc assumptions are made. Emission spectra for atoms with a single outer-trounce electron (atoms in the lithium group) tin can also be approximately predicted. Also, if the empiric electron–nuclear screening factors for many atoms are known, many other spectral lines can exist deduced from the information, in similar atoms of differing elements, via the Ritz–Rydberg combination principles (run across Rydberg formula). All these techniques substantially make use of Bohr'south Newtonian energy-potential picture of the atom.
• the relative intensities of spectral lines; although in some simple cases, Bohr's formula or modifications of it, was able to provide reasonable estimates (for instance, calculations past Kramers for the Stark effect).
• The existence of fine structure and hyperfine construction in spectral lines, which are known to be due to a variety of relativistic and subtle furnishings, as well as complications from electron spin.
• The Zeeman upshot – changes in spectral lines due to external magnetic fields; these are besides due to more complicated quantum principles interacting with electron spin and orbital magnetic fields.
• The model also violates the dubiousness principle in that it considers electrons to have known orbits and locations, two things which cannot be measured simultaneously.
• Doublets and triplets announced in the spectra of some atoms every bit very shut pairs of lines. Bohr's model cannot say why some energy levels should be very shut together.
• Multi-electron atoms do not have energy levels predicted by the model. It does non piece of work for (neutral) helium.

Refinements [edit]

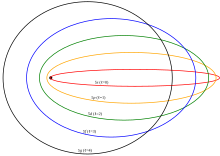
Elliptical orbits with the same free energy and quantized angular momentum

Several enhancements to the Bohr model were proposed, most notably the Sommerfeld or Bohr–Sommerfeld models, which suggested that electrons travel in elliptical orbits around a nucleus instead of the Bohr model'south circular orbits.^[1] This model supplemented the quantized angular momentum status of the Bohr model with an additional radial quantization condition, the Wilson–Sommerfeld quantization condition^{[41] [42]}

${\displaystyle \int _{0}^{T}p_{r}\,dq_{r}=nh,}$

where p_r is the radial momentum canonically conjugate to the coordinate q, which is the radial position, and T is ane full orbital flow. The integral is the action of action-bending coordinates. This condition, suggested by the correspondence principle, is the only one possible, since the quantum numbers are adiabatic invariants.

The Bohr–Sommerfeld model was fundamentally inconsistent and led to many paradoxes. The magnetic quantum number measured the tilt of the orbital aeroplane relative to the xy airplane, and information technology could only accept a few discrete values. This contradicted the obvious fact that an atom could be turned this fashion and that relative to the coordinates without restriction. The Sommerfeld quantization tin can exist performed in different canonical coordinates and sometimes gives different answers. The incorporation of radiation corrections was difficult, because information technology required finding activeness-bending coordinates for a combined radiation/atom system, which is hard when the radiations is immune to escape. The whole theory did not extend to non-integrable motions, which meant that many systems could not be treated even in principle. In the end, the model was replaced by the modern quantum-mechanical treatment of the hydrogen atom, which was get-go given by Wolfgang Pauli in 1925, using Heisenberg's matrix mechanics. The electric current moving picture of the hydrogen cantlet is based on the atomic orbitals of wave mechanics, which Erwin Schrödinger developed in 1926.

All the same, this is not to say that the Bohr–Sommerfeld model was without its successes. Calculations based on the Bohr–Sommerfeld model were able to accurately explain a number of more than complex atomic spectral effects. For example, up to outset-order perturbations, the Bohr model and quantum mechanics brand the same predictions for the spectral line splitting in the Stark outcome. At higher-order perturbations, all the same, the Bohr model and quantum mechanics differ, and measurements of the Stark consequence under high field strengths helped confirm the correctness of quantum mechanics over the Bohr model. The prevailing theory behind this difference lies in the shapes of the orbitals of the electrons, which vary according to the energy state of the electron.

The Bohr–Sommerfeld quantization weather condition lead to questions in modern mathematics. Consistent semiclassical quantization condition requires a sure type of structure on the stage space, which places topological limitations on the types of symplectic manifolds which can be quantized. In particular, the symplectic form should be the curvature form of a connection of a Hermitian line bundle, which is called a prequantization.

Bohr also updated his model in 1922, assuming that certain numbers of electrons (for instance, two, 8, and xviii) correspond to stable "closed shells".^[43]

Model of the chemical bail [edit]

Niels Bohr proposed a model of the atom and a model of the chemical bond. According to his model for a diatomic molecule, the electrons of the atoms of the molecule form a rotating ring whose airplane is perpendicular to the axis of the molecule and equidistant from the atomic nuclei. The dynamic equilibrium of the molecular system is achieved through the balance of forces between the forces of attraction of nuclei to the aeroplane of the ring of electrons and the forces of mutual repulsion of the nuclei. The Bohr model of the chemical bond took into account the Coulomb repulsion – the electrons in the ring are at the maximum distance from each other.^{[44] [45]}

See also [edit]

Wikimedia Commons has media related to Bohr model.

• 1913 in science
• Balmer's Constant
• Bohr–Sommerfeld model
• The Franck–Hertz experiment provided early support for the Bohr model.
• Free-fall diminutive model
• The inert pair effect is adequately explained by ways of the Bohr model.
• Introduction to quantum mechanics
• Theoretical and experimental justification for the Schrödinger equation

References [edit]

Footnotes [edit]

1. ^ ^{a b} Lakhtakia, Akhlesh; Salpeter, Edwin E. (1996). "Models and Modelers of Hydrogen". American Journal of Physics. 65 (9): 933. Bibcode:1997AmJPh..65..933L. doi:10.1119/1.18691.
2. ^ ^{a b} de Broglie et al. 1912, pp. 122–123.
3. ^ ^{a b c d} Kragh, Helge (1 January 1979). "Niels Bohr's Second Atomic Theory". Historical Studies in the Concrete Sciences. ten: 123–186. doi:10.2307/27757389. JSTOR 27757389.
4. ^ ^{a b c d} Bohr, N. (July 1913). "I. On the constitution of atoms and molecules". The London, Edinburgh, and Dublin Philosophical Magazine and Periodical of Scientific discipline. 26 (151): 1–25. doi:ten.1080/14786441308634955.
5. ^ Olsen, James D.; McDonald, Kirk T. (2005). "Classical lifetime of a bohr atom" (PDF). Archived (PDF) from the original on 2022-10-09. ^{[ self-published source? ]}
6. ^ "CK12 – Chemistry Flexbook Second Edition – The Bohr Model of the Atom". Retrieved 30 September 2014.
7. ^ Kragh, Helge (2012). Niels Bohr and the Quantum Cantlet: The Bohr Model of Atomic Structure 1913-1925. OUP Oxford. p. eighteen. ISBN978-0-nineteen-163046-0.
8. ^ Rayleigh, Lord (January 1906). "7. On electric vibrations and the constitution of the atom". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. eleven (61): 117–123. doi:ten.1080/14786440609463428.
9. ^ de Broglie et al. 1912, p. 114.
10. ^ ^{a b c} Heilbron, John L. (June 2013). "The path to the quantum atom". Nature. 498 (7452): 27–30. doi:x.1038/498027a. PMID 23739408. S2CID 4355108.
11. ^ de Broglie et al. 1912, p. 124.
12. ^ de Broglie et al. 1912, p. 127.
13. ^ de Broglie et al. 1912, p. 109.
14. ^ de Broglie et al. 1912, p. 447.
15. ^ ^{a b c} Heilbron, John L.; Kuhn, Thomas S. (1969). "The Genesis of the Bohr Atom". Historical Studies in the Physical Sciences. 1: half-dozen–290. doi:10.2307/27757291. JSTOR 27757291.
16. ^ ^{a b c} Niels Bohr interview 1962 Session III https://world wide web.aip.org/history-programs/niels-bohr-library/oral-histories/4517-three
17. ^ Niels Bohr interview 1962 Session Two https://www.aip.org/history-programs/niels-bohr-library/oral-histories/4517-2
18. ^ ^{a b} J. W. Nicholson, Month. Not. Roy. Astr. Soc. lxxii. pp. 49,130, 677, 693, 729 (1912).^{[ title missing ]}
19. ^ ^{a b c} McCormmach, Russell (i January 1966). "The atomic theory of John William Nicholson". Archive for History of Exact Sciences. three (ii): 160–184. doi:x.1007/BF00357268. JSTOR 41133258. S2CID 120797894.
20. ^ Hirosige, Tetu; Nisio, Sigeko (1964). "Formation of Bohr's theory of atomic constitution". Japanese Studies in the History of Science (3): 6–28. OCLC 1026682346.
21. ^ Heilbron, J. 50. (1964). A History of Atomic Models from the Discovery of the Electron to the Ancestry of Quantum Mechanics (Thesis).
22. ^ Wilson, William (November 1956). "John William Nicholson, 1881-1955". Biographical Memoirs of Fellows of the Purple Order. two: 209–214. doi:10.1098/rsbm.1956.0014.
23. ^ ^{a b} Bohr, Niels; Rosenfeld, Léon Jacques Henri Constant (1963). On the Constitution of Atoms and Molecules ... Papers of 1913 reprinted from the Philosophical Magazine, with an introduction by L. Rosenfeld. Copenhagen; W.A. Benjamin: New York. OCLC 557599205. ^{[ page needed ]}
24. ^ Stachel, John (2009). "Bohr and the Photon". Quantum Reality, Relativistic Causality, and Endmost the Epistemic Circle. Dordrecht: Springer. p. 79.
25. ^ Louisa Gilder, "The Age of Entanglement" The Arguments 1922 p. 55, "Well, yes," says Bohr. "But I tin can inappreciably imagine information technology will involve light quanta. Look, even if Einstein had found an unassailable proof of their existence and would desire to inform me past telegram, this telegram would only reach me because of the being and reality of radio waves." 2009.
26. ^ "Revealing the hidden connectedness between pi and Bohr'due south hydrogen model". Physics Globe (November 17, 2015).
27. ^ Müller, U.; de Reus, T.; Reinhardt, J.; Müller, B.; Greiner, W. (1988-03-01). "Positron production in crossed beams of bare uranium nuclei". Physical Review A. 37 (five): 1449–1455. Bibcode:1988PhRvA..37.1449M. doi:10.1103/PhysRevA.37.1449. PMID 9899816. S2CID 35364965.
28. ^ Bohr, North. (September 1913). "XXXVII. On the constitution of atoms and molecules". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 26 (153): 476–502. Bibcode:1913PMag...26..476B. doi:10.1080/14786441308634993.
29. ^ Bohr, N. (1 November 1913). "LXXIII. On the constitution of atoms and molecules". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 26 (155): 857–875. doi:x.1080/14786441308635031.
30. ^ Nicholson, J. West. (May 1914). "The Constitution of Atoms and Molecules". Nature. 93 (2324): 268–269. Bibcode:1914Natur..93..268N. doi:ten.1038/093268a0. S2CID 3977652.
31. ^ Bury, Charles R. (July 1921). "Langmuir's Theory of the Arrangement of Electrons in Atoms and Molecules". Journal of the American Chemical Lodge. 43 (seven): 1602–1609. doi:10.1021/ja01440a023.
32. ^ ^{a b} Kossel, West. (1916). "Über Molekülbildung als Frage des Atombaus" [On molecular germination as a question of atomic structure]. Annalen der Physik (in German language). 354 (3): 229–362. Bibcode:1916AnP...354..229K. doi:10.1002/andp.19163540302.
33. ^ ^{a b} Kragh, Helge (2012). "Lars Vegard, diminutive structure, and the periodic system" (PDF). Bulletin for the History of Chemistry. 37 (i): 42–49. OCLC 797965772. S2CID 53520045. Archived (PDF) from the original on 2022-ten-09.
34. ^ Langmuir, Irving (June 1919). "The Organization of Electrons in Atoms and Molecules". Journal of the American Chemical Society. 41 (6): 868–934. doi:10.1021/ja02227a002.
35. ^ "Interview of Niels Bohr past Thomas South. Kuhn, Leon Rosenfeld, Erik Rudinger, and Aage Petersen". Niels Bohr Library & Archives, American Plant of Physics. 31 Oct 1962. Retrieved 27 Mar 2019.
36. ^ Moseley, H.1000.J. (1913). "The high-frequency spectra of the elements". Philosophical Mag. sixth series. 26: 1024–1034.
37. ^ K.A.B. Whitaker (1999). "The Bohr–Moseley synthesis and a uncomplicated model for atomic x-ray energies". European Journal of Physics. twenty (3): 213–220. Bibcode:1999EJPh...20..213W. doi:10.1088/0143-0807/xx/iii/312. S2CID 250901403.
38. ^ A. van den Broek, "Die Radioelemente, das periodische Organization und die Konstitution der. Atome," Phys. Zeits, 14, 32-41 (January. 1913).
39. ^ Smith, Brian. "Quantum Ideas: Week ii" Lecture Notes, p.17. University of Oxford. Retrieved Jan. 23, 2015.
40. ^ Dahl, Jens Peder; Springborg, Michael (x Dec 1982). "Wigner's phase infinite function and atomic structure: I. The hydrogen cantlet ground state". Molecular Physics. 47 (v): 1001–1019. doi:10.1080/00268978200100752. S2CID 9628509.
41. ^ A. Sommerfeld (1916). "Zur Quantentheorie der Spektrallinien". Annalen der Physik (in German). 51 (17): i–94. Bibcode:1916AnP...356....1S. doi:10.1002/andp.19163561702.
42. ^ W. Wilson (1915). "The quantum theory of radiations and line spectra". Philosophical Magazine. 29 (174): 795–802. doi:x.1080/14786440608635362.
43. ^ Shaviv, Glora (2010). The Life of Stars: The Controversial Inception and Emergence of the Theory of Stellar Structure. Springer. p. 203. ISBN978-3642020872.
44. ^ Бор Н. (1970). Избранные научные труды (статьи 1909–1925). Vol. 1. М.: «Наука». p. 133.
45. ^ Svidzinsky, Anatoly A.; Scully, Marlan O.; Herschbach, Dudley R. (23 Baronial 2005). "Bohr's 1913 molecular model revisited". Proceedings of the National University of Sciences of the Usa. 102 (34): 11985–11988. arXiv:physics/0508161. Bibcode:2005PNAS..10211985S. doi:10.1073/pnas.0505778102. PMC1186029. PMID 16103360.

Chief sources [edit]

• Bohr, Due north. (July 1913). "I. On the constitution of atoms and molecules". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Scientific discipline. 26 (151): 1–25. doi:ten.1080/14786441308634955.
• Bohr, N. (September 1913). "XXXVII. On the constitution of atoms and molecules". The London, Edinburgh, and Dublin Philosophical Magazine and Periodical of Science. 26 (153): 476–502. Bibcode:1913PMag...26..476B. doi:10.1080/14786441308634993.
• Bohr, Due north. (1 November 1913). "LXXIII. On the constitution of atoms and molecules". The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 26 (155): 857–875. doi:10.1080/14786441308635031.
• Bohr, N. (October 1913). "The Spectra of Helium and Hydrogen". Nature. 92 (2295): 231–232. Bibcode:1913Natur..92..231B. doi:10.1038/092231d0. S2CID 11988018.
• Bohr, N. (March 1921). "Diminutive Structure". Nature. 107 (2682): 104–107. Bibcode:1921Natur.107..104B. doi:10.1038/107104a0. S2CID 4035652.
• A. Einstein (1917). "Zum Quantensatz von Sommerfeld und Epstein". Verhandlungen der Deutschen Physikalischen Gesellschaft. 19: 82–92. Reprinted in The Nerveless Papers of Albert Einstein, A. Engel translator, (1997) Princeton University Press, Princeton. half dozen p. 434. (provides an elegant reformulation of the Bohr–Sommerfeld quantization weather, also as an of import insight into the quantization of not-integrable (cluttered) dynamical systems.)
• de Broglie, Maurice; Langevin, Paul; Solvay, Ernest; Einstein, Albert (1912). La théorie du rayonnement et les quanta : rapports et discussions de la réunion tenue à Bruxelles, du 30 octobre au 3 novembre 1911, sous les auspices de One thousand.Eastward. Solvay (in French). Gauthier-Villars. OCLC 1048217622.

Further reading [edit]

• Linus Carl Pauling (1970). "Chapter v-1". Full general Chemistry (tertiary ed.). San Francisco: W.H. Freeman & Co.
  • Reprint: Linus Pauling (1988). General Chemistry . New York: Dover Publications. ISBN0-486-65622-5.
• George Gamow (1985). "Chapter 2". Thirty Years That Shook Physics. Dover Publications.
• Walter J. Lehmann (1972). "Chapter eighteen". Atomic and Molecular Construction: the development of our concepts. John Wiley and Sons. ISBN0-471-52440-9.
• Paul Tipler and Ralph Llewellyn (2002). Modern Physics (4th ed.). W. H. Freeman. ISBN0-7167-4345-0.
• Klaus Hentschel: Elektronenbahnen, Quantensprünge und Spektren, in: Charlotte Bigg & Jochen Hennig (eds.) Atombilder. Ikonografien des Atoms in Wissenschaft und Öffentlichkeit des 20. Jahrhunderts, Göttingen: Wallstein-Verlag 2009, pp. 51–61
• Steven and Susan Zumdahl (2010). "Chapter 7.4". Chemistry (8th ed.). Brooks/Cole. ISBN978-0-495-82992-8.
• Kragh, Helge (November 2011). "Conceptual objections to the Bohr atomic theory — do electrons have a 'free will'?". The European Physical Journal H. 36 (3): 327–352. Bibcode:2011EPJH...36..327K. doi:10.1140/epjh/e2011-20031-x. S2CID 120859582.

External links [edit]

• Standing waves in Bohr's diminutive model An interactive simulation to intuitively explicate the quantization condition of standing waves in Bohr's atomic mode

Wikimedia Commons has media related to Bohr model.

Who Created The Planetary Model,

Source: https://en.wikipedia.org/wiki/Bohr_model

Posted by: lopezbeforavy43.blogspot.com

Share this post